Нарисна геометрія і перспектива

Тема 2. Прямокутні проекції прямої та площини

Проекції прямої
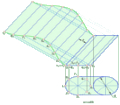
Проекції площини

Якщо точка є нульвимірною геометричною фігурою, пряма - одномірною, то площина - двовимірна геометрична фігура.

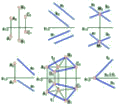
Задавати площину можуть:

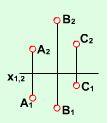
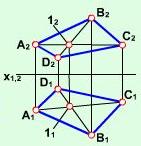
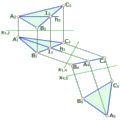
а) три точки, що не лежать на одній прямій	Рис. 2.2.1
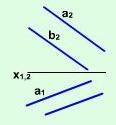
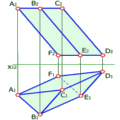
б) дві паралельні прямі	Рис. 2.2.2
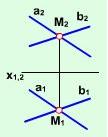
в) дві прямі, що перетинаються	Рис. 2.2.3
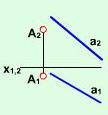
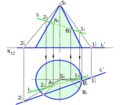
г) точка і пряма (точка не належить прямій)	Рис. 2.2.4
д) будь-яка плоска фігура	Рис. 2.2.5
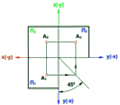
е) сліди площини	Рис. 2.2.6

Сліди площини – це лінії перетину площини з площинами проекцій.

Площини не паралельні та не перпендикулярні площинам проекцій, називаються площинами загального положення.

Площини, перпендикулярні площинам проекцій, є площинами часткового положення і називаються проекціюючими.

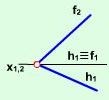
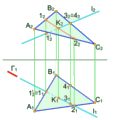
Площина, перпендикулярна до горизонтальної площини проекцій, є горизонтально проекціюючою (рис. 2.2.7).

Горизонтально проекц пл

Рис. 2.2.7

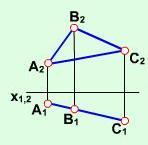
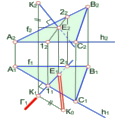
Площина, перпендикулярна до фронтальної площини проекцій, називається фронтально проекціюючою (рис. 2.2.8).

Рис. 2.2.8

А площина, перпендикулярна профільній площині проекцій, є профільно-проекціюючою (рис. 2.2.9).

Рис. 2.2.9

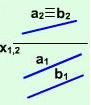
Площини, паралельні площинам проекцій, називаються площинами рівня. Відсіки площин рівня на відповідних площинах проекцій зображуються в натуральну величину. Площина, паралельна горизонтальній площині проекцій, називається горизонтальною (рис. 2.2.10), площина, паралельна фронтальній площині проекцій, називається фронтальною (рис. 2.2.11), площина, паралельна профільній площині проекцій – профільною площинами рівня (рис. 2.2.12).


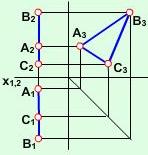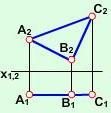
Рис. 2.2.10	Рис. 2.2.11	Рис. 2.2.12

Запитання для самоперевірки

Класифікація прямих в залежності від їх положення відносно площин проекцій.
Визначення метричних характеристик (натуральної величини, кутів нахилу до площин проекцій) відрізка прямої загального положення методом “прямокутного трикутника”.
Способи задання площини в просторі та на епюрі. Класифікація площин за їх положенням відносно площин проекцій.